 알고리즘 | 음료수 얼리기 문제 (BFS와 DFS로 각각 풀어보기)
더보기 N by M 크기의 얼음 틀이 있습니다. 구멍이 뚫려 있는 부분은 0 칸막이가 존재하는 부분은 1입니다. 구멍이 뚫려있는 부분끼리 상, 하, 좌, 우로 붙어있는 경우 서로 연결되어 있는 것으로 판단합니다. 이러한 경우에서 얼음 틀의 모양이 그래프로 주어진다면 생성되는 아이스크림의 갯수는 몇 개일까요? graph_45 = [ [0,0,1,1,0], [0,0,0,1,1], [1,1,1,1,1], [0,0,0,0,0] ] n = 4 m = 5 첫째 / BFS 방식으로 풀기 출발점에서부터 점진적으로 진행해가는 방식으로 접근하는 경우 BFS를 고려해볼 수 있습니다. 일단 BFS니까 아묻따 디큐부터 임포트해주고 시작합니다. from collections import deque 1. 함수를 작성합니다. 입력받..
2024. 4. 2.
알고리즘 | 음료수 얼리기 문제 (BFS와 DFS로 각각 풀어보기)
더보기 N by M 크기의 얼음 틀이 있습니다. 구멍이 뚫려 있는 부분은 0 칸막이가 존재하는 부분은 1입니다. 구멍이 뚫려있는 부분끼리 상, 하, 좌, 우로 붙어있는 경우 서로 연결되어 있는 것으로 판단합니다. 이러한 경우에서 얼음 틀의 모양이 그래프로 주어진다면 생성되는 아이스크림의 갯수는 몇 개일까요? graph_45 = [ [0,0,1,1,0], [0,0,0,1,1], [1,1,1,1,1], [0,0,0,0,0] ] n = 4 m = 5 첫째 / BFS 방식으로 풀기 출발점에서부터 점진적으로 진행해가는 방식으로 접근하는 경우 BFS를 고려해볼 수 있습니다. 일단 BFS니까 아묻따 디큐부터 임포트해주고 시작합니다. from collections import deque 1. 함수를 작성합니다. 입력받..
2024. 4. 2.
알고리즘 | BFS 활용하여 미로 찾기 문제 풀기
백준 2178번 미로탐색 https://www.acmicpc.net/problem/2178 2178번: 미로 탐색 첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다. www.acmicpc.net n = 4 m = 6 graph = [ [1, 0, 1, 1, 1, 1], [1, 0, 1, 0, 1, 0], [1, 0, 1, 0, 1, 1], [1, 1, 1, 0, 1, 1] ] 0과 1로 이루어진 n * m 크기의 미로 그래프가 있다. 미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동..
2024. 4. 1.
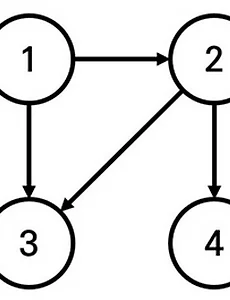 알고리즘 | BFS 활용하여 특정 도시 거리 계산 문제 풀기
https://www.acmicpc.net/problem/18352 18352번: 특정 거리의 도시 찾기 첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개 www.acmicpc.net 어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다. 이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 ..
2024. 4. 1.
알고리즘 | BFS 활용하여 특정 도시 거리 계산 문제 풀기
https://www.acmicpc.net/problem/18352 18352번: 특정 거리의 도시 찾기 첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개 www.acmicpc.net 어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다. 이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 ..
2024. 4. 1.
알고리즘 | queue(FIFO) 속도이슈를 해결할 수 있는 deque
from collections import deque 디큐는 속도가 빠른 리스트로 생각해도 좋다. 코딩 테스트에서 파이썬으로 Queue, BFS, FIFO 방식의 알고리즘 접근이 필요할 때 리스트를 디큐로 바꾸어주면 속도 이슈 해결이 가능하다. a_list = [1, 2, 3, 4, 5] # [1, 2, 3, 4, 5] a_dq = deque(a_list) # deque([1, 2, 3, 4, 5]) 이렇게 간단하게 디큐 함수로 바꾸어주기만 하면 된다. a_dq.pop() a_dq.popright() # 5 a_dq.popleft() # 1 a_dq # deque([2, 3, 4]) a_dq.append(1004) # deque([2, 3, 4, 1004]) 디큐 맨 마지막 값을 뺄 때 : .pop() ..
2024. 4. 1.
 알고리즘 | 탐색 기본, 인접행렬과 인접리스트
인접행렬 자기 자신 : 0 연결 된 엣지 : 1 (또는 1*weight) 연결 안 된 엣지 : Inf (무한대 값으로 0과 구분) # infinite 값을 선언하기 INF = float('inf') # 행렬 그래프로 나타내기 - 가중치 weight 고려해서 표현 graph = [ [0, 7, 5], [7, 0, INF], [5, INF, 0] ] 도시끼리 연결되었는지 어떻게 확인할까? graph[0][1] >>> 7 (0번과 1번 도시가 연결됨) graph[2][1] >>> inf (2번과 1번 도시가 연결 안 됨) 인접리스트 모든 노드에 연결된 노드에 대한 정보를 차례차례 연결하여 저장 # 연결된 도시만 리스트로 표현 graph = [ [(1, 7), (2, 5)], # --> 0번 도시의 연결 리스트..
2024. 4. 1.
알고리즘 | 탐색 기본, 인접행렬과 인접리스트
인접행렬 자기 자신 : 0 연결 된 엣지 : 1 (또는 1*weight) 연결 안 된 엣지 : Inf (무한대 값으로 0과 구분) # infinite 값을 선언하기 INF = float('inf') # 행렬 그래프로 나타내기 - 가중치 weight 고려해서 표현 graph = [ [0, 7, 5], [7, 0, INF], [5, INF, 0] ] 도시끼리 연결되었는지 어떻게 확인할까? graph[0][1] >>> 7 (0번과 1번 도시가 연결됨) graph[2][1] >>> inf (2번과 1번 도시가 연결 안 됨) 인접리스트 모든 노드에 연결된 노드에 대한 정보를 차례차례 연결하여 저장 # 연결된 도시만 리스트로 표현 graph = [ [(1, 7), (2, 5)], # --> 0번 도시의 연결 리스트..
2024. 4. 1.